Chapter 8 Sampling

In this chapter, we kick off the third portion of this book on statistical inference by learning about sampling. The concepts behind sampling form the basis of confidence intervals and hypothesis testing, which we’ll cover in Chapters 9 and 10. We will see that the tools that you learned in the data science portion of this book, in particular data visualization and data wrangling, will also play an important role in the development of your understanding. As mentioned before, the concepts throughout this text all build into a culmination allowing you to “tell your story with data.”

Needed packages

Let’s load all the packages needed for this chapter (this assumes you’ve already installed them). Recall from our discussion in Section 5.4 that loading the tidyverse package by running library(tidyverse) loads the following commonly used data science packages all at once:

ggplot2 for data visualization
dplyr for data wrangling
tidyr for converting data to “tidy” format
readr for importing spreadsheet data into R
As well as the more advanced purrr, tibble, stringr, and forcats packages

If needed, read Section 2.3 for information on how to install and load R packages.

library(tidyverse)
library(moderndive)

8.1 Sampling bowl activity

Let’s start with a hands-on activity.

8.1.1 What proportion of this bowl’s balls are red?

Take a look at the bowl in Figure 8.1. It has a certain number of red and a certain number of white balls all of equal size. Furthermore, it appears the bowl has been mixed beforehand, as there does not seem to be any coherent pattern to the spatial distribution of the red and white balls.

Let’s now ask ourselves, what proportion of this bowl’s balls are red?

FIGURE 8.1: A bowl with red and white balls.

One way to answer this question would be to perform an exhaustive count: remove each ball individually, count the number of red balls and the number of white balls, and divide the number of red balls by the total number of balls. However, this would be a long and tedious process.

8.1.2 Using the shovel once

Instead of performing an exhaustive count, let’s insert a shovel into the bowl as seen in Figure 8.2. Using the shovel, let’s remove $5 \cdot 10 = 50$ balls, as seen in Figure 8.3.

FIGURE 8.2: Inserting a shovel into the bowl.

FIGURE 8.3: Removing 50 balls from the bowl.

Observe that 17 of the balls are red and thus 0.34 = 34% of the shovel’s balls are red. We can view the proportion of balls that are red in this shovel as a guess of the proportion of balls that are red in the entire bowl. While not as exact as doing an exhaustive count of all the balls in the bowl, our guess of 34% took much less time and energy to make.

However, say, we started this activity over from the beginning. In other words, we replace the 50 balls back into the bowl and start over. Would we remove exactly 17 red balls again? In other words, would our guess at the proportion of the bowl’s balls that are red be exactly 34% again? Maybe?

What if we repeated this activity several times following the process shown in Figure 8.4? Would we obtain exactly 17 red balls each time? In other words, would our guess at the proportion of the bowl’s balls that are red be exactly 34% every time? Surely not. Let’s repeat this exercise several times with the help of 33 groups of friends to understand how the value differs with repetition.

8.1.3 Using the shovel 33 times

Each of our 33 groups of friends will do the following:

Use the shovel to remove 50 balls each.
Count the number of red balls and thus compute the proportion of the 50 balls that are red.
Return the balls into the bowl.
Mix the contents of the bowl a little to not let a previous group’s results influence the next group’s.

FIGURE 8.4: Repeating sampling activity 33 times.

Each of our 33 groups of friends make note of their proportion of red balls from their sample collected. Each group then marks their proportion of their 50 balls that were red in the appropriate bin in a hand-drawn histogram as seen in Figure 8.5.

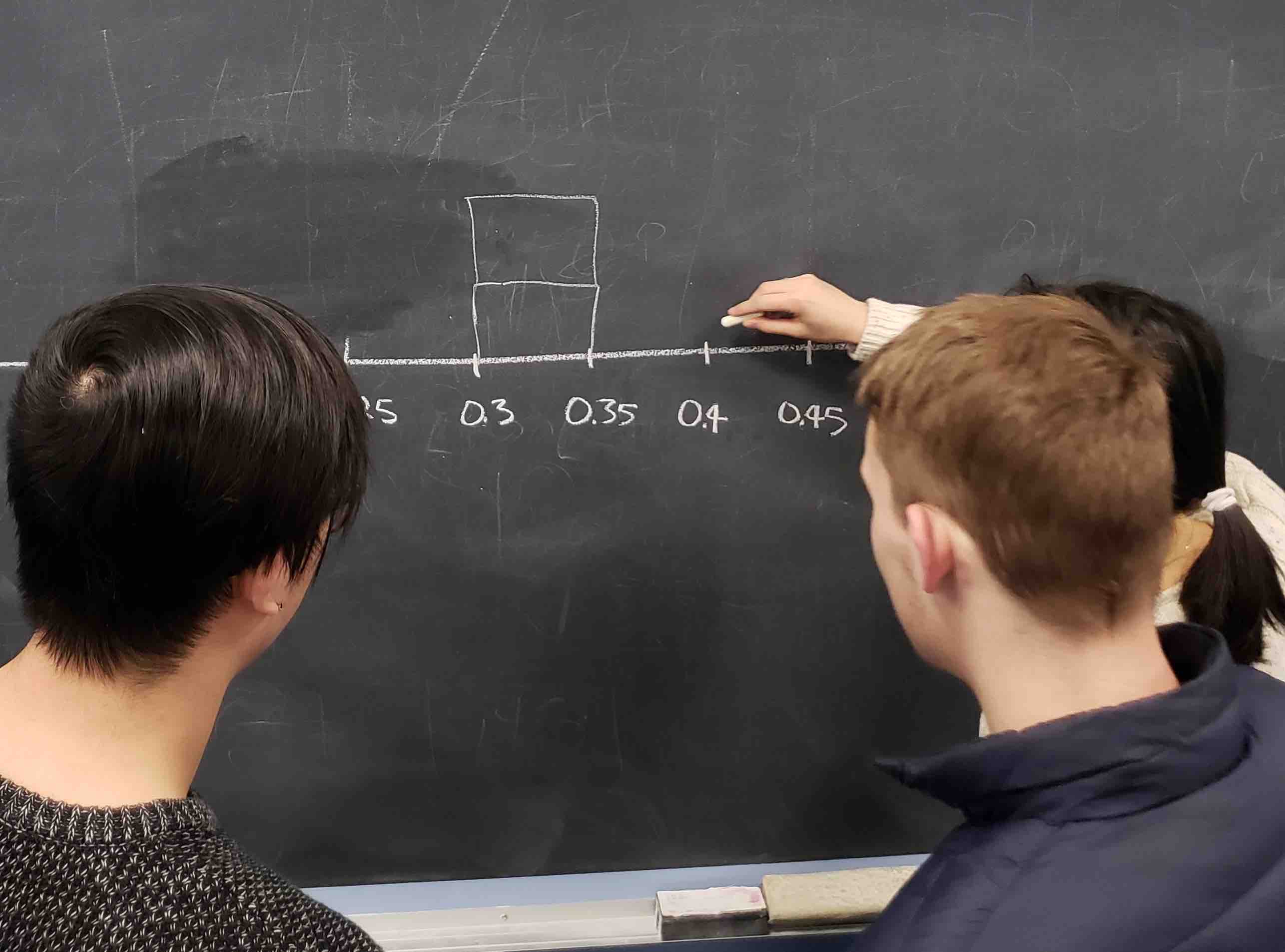
FIGURE 8.5: Constructing a histogram of proportions.

Recall from Section 3.5 that histograms allow us to visualize the distribution of a numerical variable. In particular, where the center of the values falls and how the values vary. A partially completed histogram of the first 10 out of 33 groups of friends’ results can be seen in Figure 8.6.

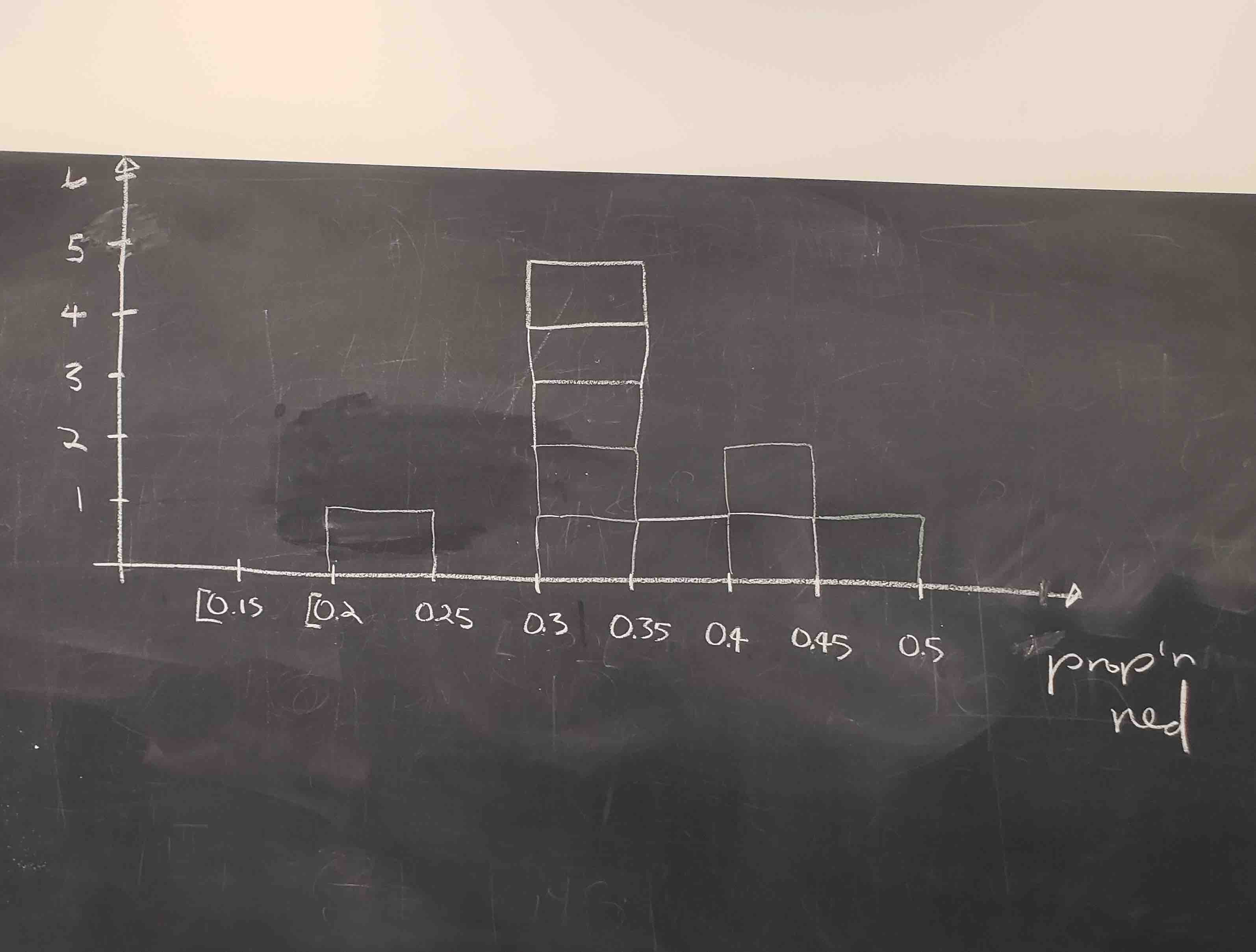
FIGURE 8.6: Hand-drawn histogram of first 10 out of 33 proportions.

Observe the following in the histogram in Figure 8.6:

At the low end, one group removed 50 balls from the bowl with proportion red between 0.20 and 0.25.
At the high end, another group removed 50 balls from the bowl with proportion between 0.45 and 0.5 red.
However, the most frequently occurring proportions were between 0.30 and 0.35 red, right in the middle of the distribution.
The shape of this distribution is somewhat bell-shaped.

Let’s construct this same hand-drawn histogram in R using your data visualization skills that you honed in Chapter 3. We saved our 33 groups of friends’ results in the tactile_prop_red data frame included in the moderndive package. Run the following to display the first 10 of 33 rows:

tactile_prop_red

# A tibble: 33 x 4
   group            replicate red_balls prop_red
   <chr>                <int>     <int>    <dbl>
 1 Ilyas, Yohan             1        21     0.42
 2 Morgan, Terrance         2        17     0.34
 3 Martin, Thomas           3        21     0.42
 4 Clark, Frank             4        21     0.42
 5 Riddhi, Karina           5        18     0.36
 6 Andrew, Tyler            6        19     0.38
 7 Julia                    7        19     0.38
 8 Rachel, Lauren           8        11     0.22
 9 Daniel, Caroline         9        15     0.3 
10 Josh, Maeve             10        17     0.34
# ... with 23 more rows

Observe for each group that we have their names, the number of red_balls they obtained, and the corresponding proportion out of 50 balls that were red named prop_red. We also have a replicate variable enumerating each of the 33 groups. We chose this name because each row can be viewed as one instance of a replicated (in other words repeated) activity: using the shovel to remove 50 balls and computing the proportion of those balls that are red.

Let’s visualize the distribution of these 33 proportions using geom_histogram() with binwidth = 0.05 in Figure 8.7. This is a computerized and complete version of the partially completed hand-drawn histogram you saw in Figure 8.6. Note that setting boundary = 0.4 indicates that we want a binning scheme such that one of the bins’ boundary is at 0.4. This helps us to more closely align this histogram with the hand-drawn histogram in Figure 8.6.

ggplot(tactile_prop_red, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 50 balls that were red", 
       title = "Distribution of 33 proportions red")

FIGURE 8.7: Distribution of 33 proportions based on 33 samples of size 50.

8.1.4 What did we just do?

What we just demonstrated in this activity is the statistical concept of sampling. We would like to know the proportion of the bowl’s balls that are red. Because the bowl has a large number of balls, performing an exhaustive count of the red and white balls would be time-consuming. We thus extracted a sample of 50 balls using the shovel to make an estimate. Using this sample of 50 balls, we estimated the proportion of the bowl’s balls that are red to be 34%.

Moreover, because we mixed the balls before each use of the shovel, the samples were randomly drawn. Because each sample was drawn at random, the samples were different from each other. Because the samples were different from each other, we obtained the different proportions red observed in Figure 8.7. This is known as the concept of sampling variation.

The purpose of this sampling activity was to develop an understanding of two key concepts relating to sampling:

Understanding the effect of sampling variation.
Understanding the effect of sample size on sampling variation.

In Section 8.2, we’ll mimic the hands-on sampling activity we just performed on a computer. This will allow us not only to repeat the sampling exercise much more than 33 times, but it will also allow us to use shovels with different numbers of slots than just 50.

Afterwards, we’ll present you with definitions, terminology, and notation related to sampling in Section 8.3. As in many disciplines, such necessary background knowledge may seem inaccessible and even confusing at first. However, as with many difficult topics, if you truly understand the underlying concepts and practice, practice, practice, you’ll be able to master them.

To tie the contents of this chapter to the real world, we’ll present an example of one of the most recognizable uses of sampling: polls. In Section 8.4 we’ll look at a particular case study: a 2013 poll on then U.S. President Barack Obama’s popularity among young Americans, conducted by Kennedy School’s Institute of Politics at Harvard University. To close this chapter, we’ll generalize the “sampling from a bowl” exercise to other sampling scenarios and present a theoretical result known as the Central Limit Theorem.

Learning check

(LC7.1) Why was it important to mix the bowl before we sampled the balls?

(LC7.2) Why is it that our 33 groups of friends did not all have the same numbers of balls that were red out of 50, and hence different proportions red?

8.2 Virtual sampling

In the previous Section 8.1, we performed a tactile sampling activity by hand. In other words, we used a physical bowl of balls and a physical shovel. We performed this sampling activity by hand first so that we could develop a firm understanding of the root ideas behind sampling. In this section, we’ll mimic this tactile sampling activity with a virtual sampling activity using a computer. In other words, we’ll use a virtual analog to the bowl of balls and a virtual analog to the shovel.

8.2.1 Using the virtual shovel once

Let’s start by performing the virtual analog of the tactile sampling exercise we performed in Section 8.1. We first need a virtual analog of the bowl seen in Figure 8.1. To this end, we included a data frame named bowl in the moderndive package. The rows of bowl correspond exactly with the contents of the actual bowl.

bowl

# A tibble: 2,400 x 2
   ball_ID color
     <int> <chr>
 1       1 white
 2       2 white
 3       3 white
 4       4 red  
 5       5 white
 6       6 white
 7       7 red  
 8       8 white
 9       9 red  
10      10 white
# ... with 2,390 more rows

Observe that bowl has 2400 rows, telling us that the bowl contains 2400 equally sized balls. The first variable ball_ID is used as an identification variable as discussed in Subsection 2.4.4; none of the balls in the actual bowl are marked with numbers. The second variable color indicates whether a particular virtual ball is red or white. View the contents of the bowl in RStudio’s data viewer and scroll through the contents to convince yourself that bowl is indeed a virtual analog of the actual bowl in Figure 8.1.

Now that we have a virtual analog of our bowl, we now need a virtual analog to the shovel seen in Figure 8.2 to generate virtual samples of 50 balls. We’re going to use the rep_sample_n() function included in the moderndive package. This function allows us to take repeated, or replicated, samples of size n.

virtual_shovel <- bowl %>% 
  rep_sample_n(size = 50)
virtual_shovel

# A tibble: 50 x 3
# Groups:   replicate [1]
   replicate ball_ID color
       <int>   <int> <chr>
 1         1    1970 white
 2         1     842 red  
 3         1    2287 white
 4         1     599 white
 5         1     108 white
 6         1     846 red  
 7         1     390 red  
 8         1     344 white
 9         1     910 white
10         1    1485 white
# ... with 40 more rows

Observe that virtual_shovel has 50 rows corresponding to our virtual sample of size 50. The ball_ID variable identifies which of the 2400 balls from bowl are included in our sample of 50 balls while color denotes its color. However, what does the replicate variable indicate? In virtual_shovel’s case, replicate is equal to 1 for all 50 rows. This is telling us that these 50 rows correspond to the first repeated/replicated use of the shovel, in our case our first sample. We’ll see shortly that when we “virtually” take 33 samples, replicate will take values between 1 and 33.

Let’s compute the proportion of balls in our virtual sample that are red using the dplyr data wrangling verbs you learned in Chapter 4. First, for each of our 50 sampled balls, let’s identify if it is red or not using a test for equality with ==. Let’s create a new Boolean variable is_red using the mutate() function from Section 4.5:

virtual_shovel %>% 
  mutate(is_red = (color == "red"))

# A tibble: 50 x 4
# Groups:   replicate [1]
   replicate ball_ID color is_red
       <int>   <int> <chr> <lgl> 
 1         1    1970 white FALSE 
 2         1     842 red   TRUE  
 3         1    2287 white FALSE 
 4         1     599 white FALSE 
 5         1     108 white FALSE 
 6         1     846 red   TRUE  
 7         1     390 red   TRUE  
 8         1     344 white FALSE 
 9         1     910 white FALSE 
10         1    1485 white FALSE 
# ... with 40 more rows

Observe that for every row where color == "red", the Boolean (logical) value TRUE is returned and for every row where color is not equal to "red", the Boolean FALSE is returned.

Second, let’s compute the number of balls out of 50 that are red using the summarize() function. Recall from Section 4.3 that summarize() takes a data frame with many rows and returns a data frame with a single row containing summary statistics, like the mean() or median(). In this case, we use the sum():

virtual_shovel %>% 
  mutate(is_red = (color == "red")) %>% 
  summarize(num_red = sum(is_red))

# A tibble: 1 x 2
  replicate num_red
      <int>   <int>
1         1      12

Why does this work? Because R treats TRUE like the number 1 and FALSE like the number 0. So summing the number of TRUEs and FALSEs is equivalent to summing 1’s and 0’s. In the end, this operation counts the number of balls where color is red. In our case, 12 of the 50 balls were red. However, you might have gotten a different number red because of the randomness of the virtual sampling.

Third and lastly, let’s compute the proportion of the 50 sampled balls that are red by dividing num_red by 50:

virtual_shovel %>% 
  mutate(is_red = color == "red") %>% 
  summarize(num_red = sum(is_red)) %>% 
  mutate(prop_red = num_red / 50)

# A tibble: 1 x 3
  replicate num_red prop_red
      <int>   <int>    <dbl>
1         1      12     0.24

In other words, 24% of this virtual sample’s balls were red. Let’s make this code a little more compact and succinct by combining the first mutate() and the summarize() as follows:

virtual_shovel %>% 
  summarize(num_red = sum(color == "red")) %>% 
  mutate(prop_red = num_red / 50)

# A tibble: 1 x 3
  replicate num_red prop_red
      <int>   <int>    <dbl>
1         1      12     0.24

Great! 24% of virtual_shovel’s 50 balls were red! So based on this particular sample of 50 balls, our guess at the proportion of the bowl’s balls that are red is 24%. But remember from our earlier tactile sampling activity that if we repeat this sampling, we will not necessarily obtain the same value of 24% again. There will likely be some variation. In fact, our 33 groups of friends computed 33 such proportions whose distribution we visualized in Figure 8.6. We saw that these estimates varied. Let’s now perform the virtual analog of having 33 groups of students use the sampling shovel!

8.2.2 Using the virtual shovel 33 times

Recall that in our tactile sampling exercise in Section 8.1, we had 33 groups of students each use the shovel, yielding 33 samples of size 50 balls. We then used these 33 samples to compute 33 proportions. In other words, we repeated/replicated using the shovel 33 times. We can perform this repeated/replicated sampling virtually by once again using our virtual shovel function rep_sample_n(), but by adding the reps = 33 argument. This is telling R that we want to repeat the sampling 33 times.

We’ll save these results in a data frame called virtual_samples. While we provide a preview of the first 10 rows of virtual_samples in what follows, we highly suggest you scroll through its contents using RStudio’s spreadsheet viewer by running View(virtual_samples).

virtual_samples <- bowl %>% 
  rep_sample_n(size = 50, reps = 33)
virtual_samples

# A tibble: 1,650 x 3
# Groups:   replicate [33]
   replicate ball_ID color
       <int>   <int> <chr>
 1         1     875 white
 2         1    1851 red  
 3         1    1548 red  
 4         1    1975 white
 5         1     835 white
 6         1      16 white
 7         1     327 white
 8         1    1803 red  
 9         1     740 red  
10         1     179 red  
# ... with 1,640 more rows

Observe in the spreadsheet viewer that the first 50 rows of replicate are equal to 1 while the next 50 rows of replicate are equal to 2. This is telling us that the first 50 rows correspond to the first sample of 50 balls while the next 50 rows correspond to the second sample of 50 balls. This pattern continues for all reps = 33 replicates and thus virtual_samples has 33 $\cdot$ 50 = 1650 rows.

Let’s now take virtual_samples and compute the resulting 33 proportions red. We’ll use the same dplyr verbs as before, but this time with an additional group_by() of the replicate variable. Recall from Section 4.4 that by assigning the grouping variable “meta-data” before we summarize(), we’ll obtain 33 different proportions red. We display a preview of the first 10 out of 33 rows:

virtual_prop_red <- virtual_samples %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 50)
virtual_prop_red

# A tibble: 33 x 3
   replicate   red prop_red
       <int> <int>    <dbl>
 1         1    23     0.46
 2         2    19     0.38
 3         3    18     0.36
 4         4    19     0.38
 5         5    15     0.3 
 6         6    21     0.42
 7         7    21     0.42
 8         8    16     0.32
 9         9    24     0.48
10        10    14     0.28
# ... with 23 more rows

As with our 33 groups of friends’ tactile samples, there is variation in the resulting 33 virtual proportions red. Let’s visualize this variation in a histogram in Figure 8.8. Note that we add binwidth = 0.05 and boundary = 0.4 arguments as well. Recall that setting boundary = 0.4 ensures a binning scheme with one of the bins’ boundaries at 0.4. Since the binwidth = 0.05 is also set, this will create bins with boundaries at 0.30, 0.35, 0.45, 0.5, etc. as well.

ggplot(virtual_prop_red, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 50 balls that were red", 
       title = "Distribution of 33 proportions red")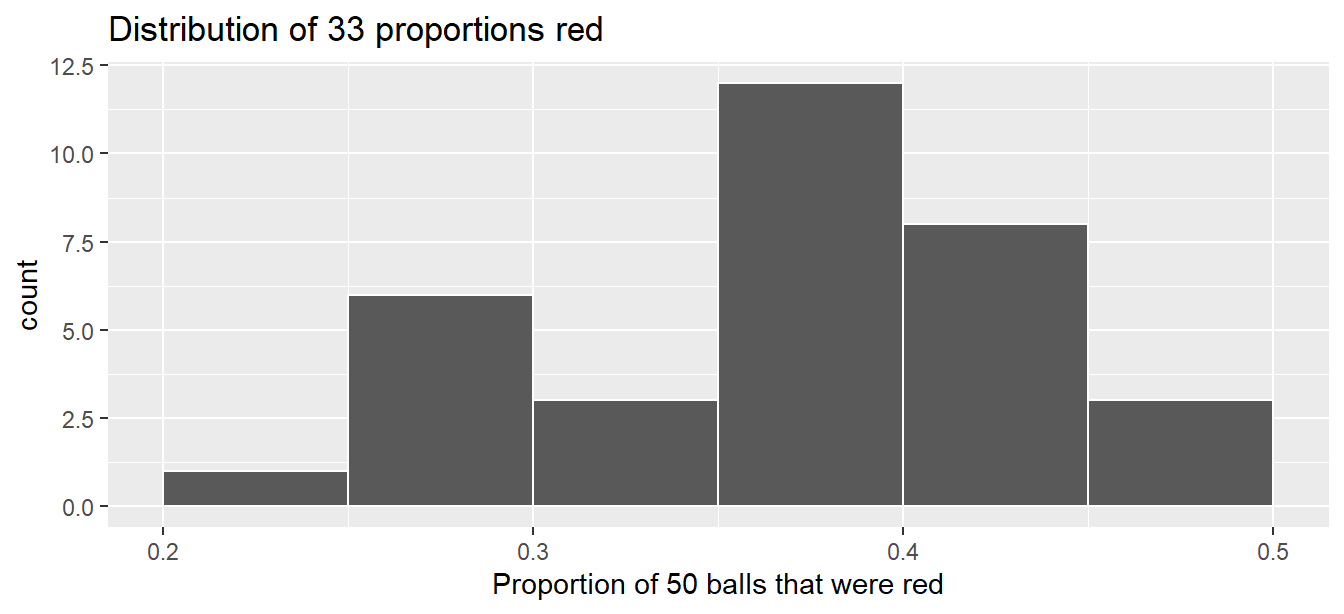

FIGURE 8.8: Distribution of 33 proportions based on 33 samples of size 50.

Observe that we occasionally obtained proportions red that are less than 30%. On the other hand, we occasionally obtained proportions that are greater than 45%. However, the most frequently occurring proportions were between 35% and 40% (for 11 out of 33 samples). Why do we have these differences in proportions red? Because of sampling variation.

Let’s now compare our virtual results with our tactile results from the previous section in Figure 8.9. Observe that both histograms are somewhat similar in their center and variation, although not identical. These slight differences are again due to random sampling variation. Furthermore, observe that both distributions are somewhat bell-shaped.

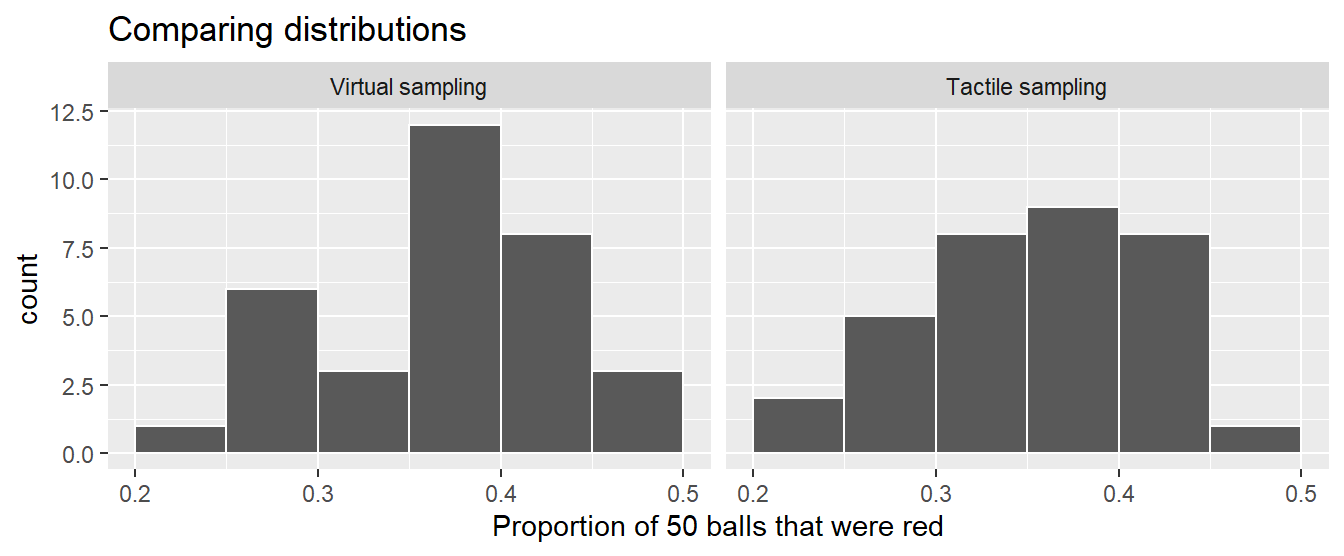
FIGURE 8.9: Comparing 33 virtual and 33 tactile proportions red.

Learning check

(LC7.3) Why couldn’t we study the effects of sampling variation when we used the virtual shovel only once? Why did we need to take more than one virtual sample (in our case 33 virtual samples)?

8.2.3 Using the virtual shovel 1000 times

Now say we want to study the effects of sampling variation not for 33 samples, but rather for a larger number of samples, say 1000. We have two choices at this point. We could have our groups of friends manually take 1000 samples of 50 balls and compute the corresponding 1000 proportions. However, this would be a tedious and time-consuming task. This is where computers excel: automating long and repetitive tasks while performing them quite quickly. Thus, at this point we will abandon tactile sampling in favor of only virtual sampling. Let’s once again use the rep_sample_n() function with sample size set to be 50 once again, but this time with the number of replicates reps set to 1000. Be sure to scroll through the contents of virtual_samples in RStudio’s viewer.

virtual_samples <- bowl %>% 
  rep_sample_n(size = 50, reps = 1000)
virtual_samples

# A tibble: 50,000 x 3
# Groups:   replicate [1,000]
   replicate ball_ID color
       <int>   <int> <chr>
 1         1    1236 red  
 2         1    1944 red  
 3         1    1939 white
 4         1     780 white
 5         1    1956 white
 6         1    1003 white
 7         1    2113 white
 8         1    2213 white
 9         1     782 white
10         1     898 white
# ... with 49,990 more rows

Observe that now virtual_samples has 1000 $\cdot$ 50 = 50,000 rows, instead of the 33 $\cdot$ 50 = 1650 rows from earlier. Using the same data wrangling code as earlier, let’s take the data frame virtual_samples with 1000 $\cdot$ 50 = 50,000 rows and compute the resulting 1000 proportions of red balls.

virtual_prop_red <- virtual_samples %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 50)
virtual_prop_red

# A tibble: 1,000 x 3
   replicate   red prop_red
       <int> <int>    <dbl>
 1         1    18     0.36
 2         2    19     0.38
 3         3    20     0.4 
 4         4    15     0.3 
 5         5    17     0.34
 6         6    16     0.32
 7         7    23     0.46
 8         8    23     0.46
 9         9    15     0.3 
10        10    18     0.36
# ... with 990 more rows

Observe that we now have 1000 replicates of prop_red, the proportion of 50 balls that are red. Using the same code as earlier, let’s now visualize the distribution of these 1000 replicates of prop_red in a histogram in Figure 8.10.

ggplot(virtual_prop_red, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 50 balls that were red", 
       title = "Distribution of 1000 proportions red")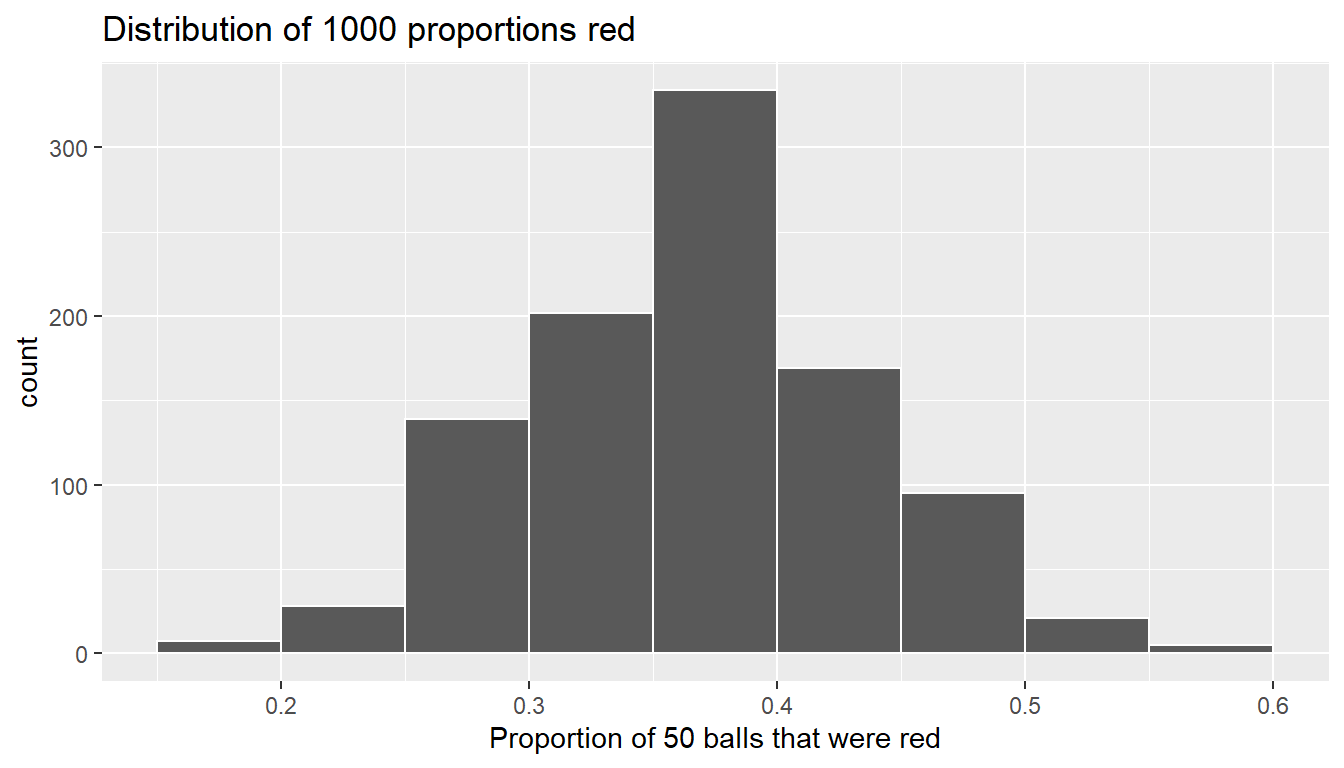

FIGURE 8.10: Distribution of 1000 proportions based on 1000 samples of size 50.

Once again, the most frequently occurring proportions of red balls occur between 35% and 40%. Every now and then, we obtain proportions as low as between 20% and 25%, and others as high as between 55% and 60%. These are rare, however. Furthermore, observe that we now have a much more symmetric and smoother bell-shaped distribution. This distribution is, in fact, approximated well by a normal distribution. At this point we recommend you read the “Normal distribution” section (Appendix A.2) for a brief discussion on the properties of the normal distribution.

Learning check

(LC7.4) Why did we not take 1000 “tactile” samples of 50 balls by hand?

(LC7.5) Looking at Figure 8.10, would you say that sampling 50 balls where 30% of them were red is likely or not? What about sampling 50 balls where 10% of them were red?

8.2.4 Using different shovels

Now say instead of just one shovel, you have three choices of shovels to extract a sample of balls with: shovels of size 25, 50, and 100.

FIGURE 8.11: Three shovels to extract three different sample sizes.

If your goal is still to estimate the proportion of the bowl’s balls that are red, which shovel would you choose? In our experience, most people would choose the largest shovel with 100 slots because it would yield the “best” guess of the proportion of the bowl’s balls that are red. Let’s define some criteria for “best” in this subsection.

Using our newly developed tools for virtual sampling, let’s unpack the effect of having different sample sizes! In other words, let’s use rep_sample_n() with size set to 25, 50, and 100, respectively, while keeping the number of repeated/replicated samples at 1000:

Virtually use the appropriate shovel to generate 1000 samples with size balls.
Compute the resulting 1000 replicates of the proportion of the shovel’s balls that are red.
Visualize the distribution of these 1000 proportions red using a histogram.

Run each of the following code segments individually and then compare the three resulting histograms.

# Segment 1: sample size = 25 ------------------------------
# 1.a) Virtually use shovel 1000 times
virtual_samples_25 <- bowl %>% 
  rep_sample_n(size = 25, reps = 1000)

# 1.b) Compute resulting 1000 replicates of proportion red
virtual_prop_red_25 <- virtual_samples_25 %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 25)

# 1.c) Plot distribution via a histogram
ggplot(virtual_prop_red_25, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 25 balls that were red", title = "25") 


# Segment 2: sample size = 50 ------------------------------
# 2.a) Virtually use shovel 1000 times
virtual_samples_50 <- bowl %>% 
  rep_sample_n(size = 50, reps = 1000)

# 2.b) Compute resulting 1000 replicates of proportion red
virtual_prop_red_50 <- virtual_samples_50 %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 50)

# 2.c) Plot distribution via a histogram
ggplot(virtual_prop_red_50, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 50 balls that were red", title = "50")  


# Segment 3: sample size = 100 ------------------------------
# 3.a) Virtually using shovel with 100 slots 1000 times
virtual_samples_100 <- bowl %>% 
  rep_sample_n(size = 100, reps = 1000)

# 3.b) Compute resulting 1000 replicates of proportion red
virtual_prop_red_100 <- virtual_samples_100 %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 100)

# 3.c) Plot distribution via a histogram
ggplot(virtual_prop_red_100, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 100 balls that were red", title = "100")

For easy comparison, we present the three resulting histograms in a single row with matching x and y axes in Figure 8.12.

FIGURE 8.12: Comparing the distributions of proportion red for different sample sizes.

Observe that as the sample size increases, the variation of the 1000 replicates of the proportion of red decreases. In other words, as the sample size increases, there are fewer differences due to sampling variation and the distribution centers more tightly around the same value. Eyeballing Figure 8.12, all three histograms appear to center around roughly 40%.

We can be numerically explicit about the amount of variation in our three sets of 1000 values of prop_red using the standard deviation. A standard deviation is a summary statistic that measures the amount of variation within a numerical variable (see Appendix A.1 for a brief discussion on the properties of the standard deviation). For all three sample sizes, let’s compute the standard deviation of the 1000 proportions red by running the following data wrangling code that uses the sd() summary function.

# n = 25
virtual_prop_red_25 %>% 
  summarize(sd = sd(prop_red))

# n = 50
virtual_prop_red_50 %>% 
  summarize(sd = sd(prop_red))

# n = 100
virtual_prop_red_100 %>% 
  summarize(sd = sd(prop_red))

Let’s compare these three measures of distributional variation in Table 8.1.

TABLE 8.1: Comparing standard deviations of proportions red for three different shovels
Number of slots in shovel	Standard deviation of proportions red
25	0.094
50	0.069
100	0.045

As we observed in Figure 8.12, as the sample size increases, the variation decreases. In other words, there is less variation in the 1000 values of the proportion red. So as the sample size increases, our guesses at the true proportion of the bowl’s balls that are red get more precise.

Learning check

(LC7.6) In Figure 8.12, we used shovels to take 1000 samples each, computed the resulting 1000 proportions of the shovel’s balls that were red, and then visualized the distribution of these 1000 proportions in a histogram. We did this for shovels with 25, 50, and 100 slots in them. As the size of the shovels increased, the histograms got narrower. In other words, as the size of the shovels increased from 25 to 50 to 100, did the 1000 proportions

A. vary less,
B. vary by the same amount, or
C. vary more?

(LC7.7) What summary statistic did we use to quantify how much the 1000 proportions red varied?

A. The interquartile range
B. The standard deviation
C. The range: the largest value minus the smallest.

8.3 Sampling framework

In both our tactile and our virtual sampling activities, we used sampling for the purpose of estimation. We extracted samples in order to estimate the proportion of the bowl’s balls that are red. We used sampling as a less time-consuming approach than performing an exhaustive count of all the balls. Our virtual sampling activity built up to the results shown in Figure 8.12 and Table 8.1: comparing 1000 proportions red based on samples of size 25, 50, and 100. This was our first attempt at understanding two key concepts relating to sampling for estimation:

The effect of sampling variation on our estimates.
The effect of sample size on sampling variation.

Let’s now introduce some terminology and notation as well as statistical definitions related to sampling. Given the number of new words you’ll need to learn, you will likely have to read this section a few times. Keep in mind, however, that all of the concepts underlying these terminology, notation, and definitions tie directly to the concepts underlying our tactile and virtual sampling activities. It will simply take time and practice to master them.

8.3.1 Terminology and notation

Here is a list of terminology and mathematical notation relating to sampling.

First, a population is a collection of individuals or observations we are interested in. This is also commonly denoted as a study population. We mathematically denote the population’s size using upper-case $N$. In our sampling activities, the (study) population is the collection of $N$ = 2400 identically sized red and white balls contained in the bowl.

Second, a population parameter is a numerical summary quantity about the population that is unknown, but you wish you knew. For example, when this quantity is a mean, the population parameter of interest is the population mean. This is mathematically denoted with the Greek letter $\mu$ pronounced “mu” (we’ll see a sampling activity involving means in the upcoming Section 9.1). In our earlier sampling from the bowl activity, however, since we were interested in the proportion of the bowl’s balls that were red, the population parameter is the population proportion. This is mathematically denoted with the letter $p$.

Third, a census is an exhaustive enumeration or counting of all $N$ individuals or observations in the population in order to compute the population parameter’s value exactly. In our sampling activity, this would correspond to counting the number of balls out of $N$ = 2400 that are red and computing the population proportion $p$ that are red exactly. When the number $N$ of individuals or observations in our population is large as was the case with our bowl, a census can be quite expensive in terms of time, energy, and money.

Fourth, sampling is the act of collecting a sample from the population when we don’t have the means to perform a census. We mathematically denote the sample’s size using lower case $n$, as opposed to upper case $N$ which denotes the population’s size. Typically the sample size $n$ is much smaller than the population size $N$. Thus sampling is a much cheaper alternative than performing a census. In our sampling activities, we used shovels with 25, 50, and 100 slots to extract samples of size $n$ = 25, $n$ = 50, and $n$ = 100.

Fifth, a point estimate (AKA sample statistic) is a summary statistic computed from a sample that estimates an unknown population parameter. In our sampling activities, recall that the unknown population parameter was the population proportion and that this is mathematically denoted with $p$. Our point estimate is the sample proportion: the proportion of the shovel’s balls that are red. In other words, it is our guess of the proportion of the bowl’s balls that are red. We mathematically denote the sample proportion using $\widehat{p}$. The “hat” on top of the $p$ indicates that it is an estimate of the unknown population proportion $p$.

Sixth is the idea of representative sampling. A sample is said to be a representative sample if it roughly looks like the population. In other words, are the sample’s characteristics a good representation of the population’s characteristics? In our sampling activity, are the samples of $n$ balls extracted using our shovels representative of the bowl’s $N$ = 2400 balls?

Seventh is the idea of generalizability. We say a sample is generalizable if any results based on the sample can generalize to the population. In other words, does the value of the point estimate generalize to the population? In our sampling activity, can we generalize the sample proportion from our shovels to the entire bowl? Using our mathematical notation, this is akin to asking if $\widehat{p}$ is a “good guess” of $p$?

Eighth, we say biased sampling occurs if certain individuals or observations in a population have a higher chance of being included in a sample than others. We say a sampling procedure is unbiased if every observation in a population had an equal chance of being sampled. In our sampling activities, since we mixed all $N = 2400$ balls prior to each group’s sampling and since each of the equally sized balls had an equal chance of being sampled, our samples were unbiased.

Ninth and lastly, the idea of random sampling. We say a sampling procedure is random if we sample randomly from the population in an unbiased fashion. In our sampling activities, this would correspond to sufficiently mixing the bowl before each use of the shovel.

Phew, that’s a lot of new terminology and notation to learn! Let’s put them all together to describe the paradigm of sampling.

In general:

If the sampling of a sample of size $n$ is done at random, then
the sample is unbiased and representative of the population of size $N$, thus
any result based on the sample can generalize to the population, thus
the point estimate is a “good guess” of the unknown population parameter, thus
instead of performing a census, we can infer about the population using sampling.

Specific to our sampling activity:

If we extract a sample of $n=50$ balls at random, in other words, we mix all of the equally sized balls before using the shovel, then
the contents of the shovel are an unbiased representation of the contents of the bowl’s 2400 balls, thus
any result based on the shovel’s balls can generalize to the bowl, thus
the sample proportion $\widehat{p}$ of the $n=50$ balls in the shovel that are red is a “good guess” of the population proportion $p$ of the $N=2400$ balls that are red, thus
instead of manually going over all 2400 balls in the bowl, we can infer about the bowl using the shovel.

Note that last word we wrote in bold: infer. The act of “inferring” means to deduce or conclude information from evidence and reasoning. In our sampling activities, we wanted to infer about the proportion of the bowl’s balls that are red. Statistical inference is the “theory, methods, and practice of forming judgments about the parameters of a population and the reliability of statistical relationships, typically on the basis of random sampling.” In other words, statistical inference is the act of inference via sampling. In the upcoming Chapter 9 on confidence intervals, we’ll introduce the infer package, which makes statistical inference “tidy” and transparent. It is why this third portion of the book is called “Statistical inference via infer.”

Learning check

(LC7.8) In the case of our bowl activity, what is the population parameter? Do we know its value?

(LC7.9) What would performing a census in our bowl activity correspond to? Why did we not perform a census?

(LC7.10) What purpose do point estimates serve in general? What is the name of the point estimate specific to our bowl activity? What is its mathematical notation?

(LC7.11) How did we ensure that our tactile samples using the shovel were random?

(LC7.12) Why is it important that sampling be done at random?

(LC7.13) What are we inferring about the bowl based on the samples using the shovel?

8.3.2 Statistical definitions

Now, for some important statistical definitions related to sampling. As a refresher of our 1000 repeated/replicated virtual samples of size $n$ = 25, $n$ = 50, and $n$ = 100 in Section 8.2, let’s display Figure 8.12 again as Figure 8.13.

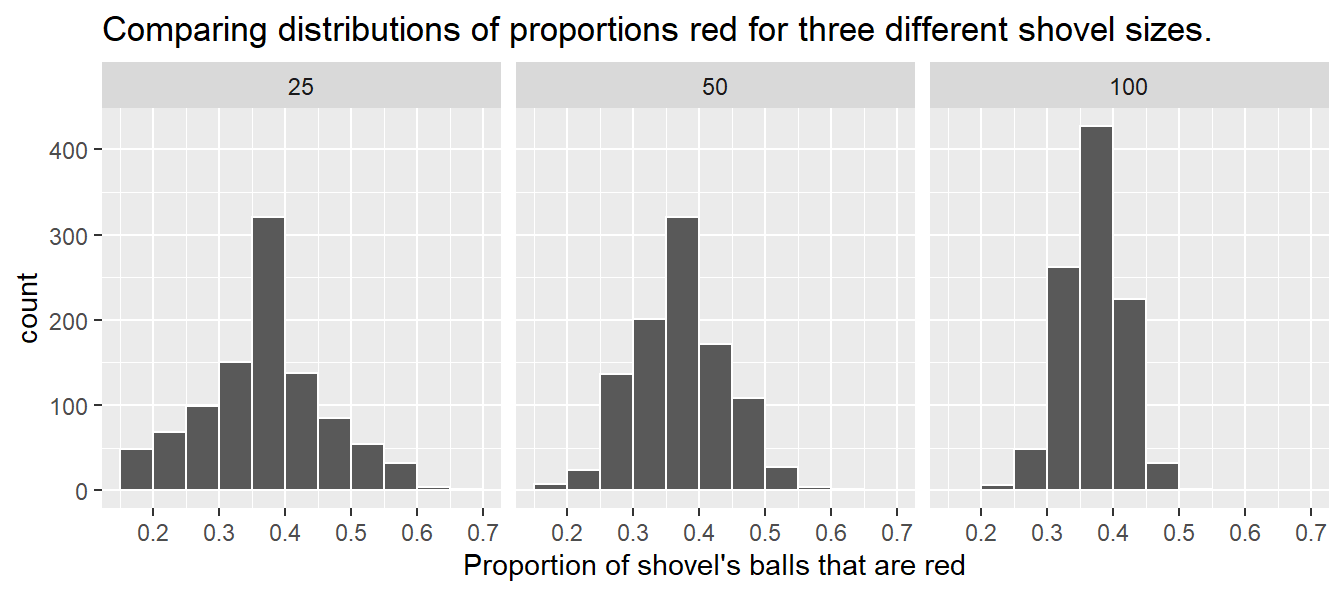
$Previously seen three distributions of the sample proportion $\widehat{p}$.$

FIGURE 8.13: Previously seen three distributions of the sample proportion $\widehat{p}$.

These types of distributions have a special name: sampling distributions; their visualization displays the effect of sampling variation on the distribution of any point estimate, in this case, the sample proportion $\widehat{p}$. Using these sampling distributions, for a given sample size $n$, we can make statements about what values we can typically expect.

For example, observe the centers of all three sampling distributions: they are all roughly centered around $0.4 = 40\%$. Furthermore, observe that while we are somewhat likely to observe sample proportions of red balls of $0.2 = 20\%$ when using the shovel with 25 slots, we will almost never observe a proportion of 20% when using the shovel with 100 slots. Observe also the effect of sample size on the sampling variation. As the sample size $n$ increases from 25 to 50 to 100, the variation of the sampling distribution decreases and thus the values cluster more and more tightly around the same center of around 40%. We quantified this variation using the standard deviation of our sample proportions in Table 8.1, which we display again as Table 8.2:

TABLE 8.2: Previously seen comparing standard deviations of proportions red for three different shovels
Number of slots in shovel	Standard deviation of proportions red
25	0.094
50	0.069
100	0.045

So as the sample size increases, the standard deviation of the proportion of red balls decreases. This type of standard deviation has another special name: standard error. Standard errors quantify the effect of sampling variation induced on our estimates. In other words, they quantify how much we can expect different proportions of a shovel’s balls that are red to vary from one sample to another sample to another sample, and so on. As a general rule, as sample size increases, the standard error decreases.

Unfortunately, these names confuse many people who are new to statistical inference. For example, it’s common for people who are new to statistical inference to call the “sampling distribution” the “sample distribution.” Another additional source of confusion is the name “standard deviation” and “standard error.” Remember that a standard error is merely a kind of standard deviation: the standard deviation of any point estimate from sampling. In other words, all standard errors are standard deviations, but not every standard deviation is necessarily a standard error.

To help reinforce these concepts, let’s re-display Figure 8.12 but using our new terminology, notation, and definitions relating to sampling in Figure 8.14.

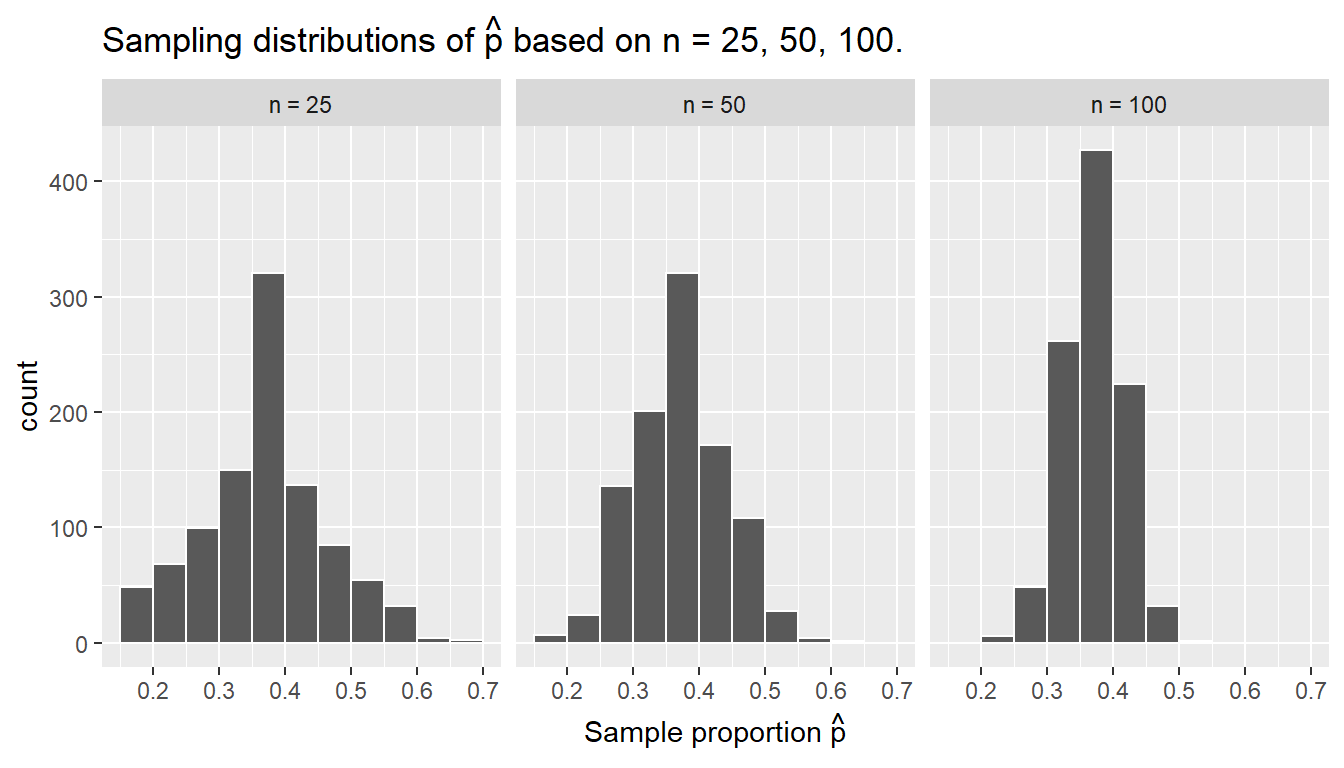
$Three sampling distributions of the sample proportion $\widehat{p}$.$

FIGURE 8.14: Three sampling distributions of the sample proportion $\widehat{p}$.

Furthermore, let’s re-display Table 8.1 but using our new terminology, notation, and definitions relating to sampling in Table 8.3.

TABLE 8.3: Standard errors of the sample proportion based on sample sizes of 25, 50, and 100
Sample size (n)	Standard error of $\widehat{p}$
n = 25	0.094
n = 50	0.069
n = 100	0.045

Remember the key message of this last table: that as the sample size $n$ goes up, the “typical” error of your point estimate will go down, as quantified by the standard error.

Learning check

(LC7.14) What purpose did the sampling distributions serve?

(LC7.15) What does the standard error of the sample proportion $\widehat{p}$ quantify?

8.3.3 The moral of the story

Let’s recap this section so far. We’ve seen that if a sample is generated at random, then the resulting point estimate is a “good guess” of the true unknown population parameter. In our sampling activities, since we made sure to mix the balls first before extracting a sample with the shovel, the resulting sample proportion $\widehat{p}$ of the shovel’s balls that were red was a “good guess” of the population proportion $p$ of the bowl’s balls that were red.

However, what do we mean by our point estimate being a “good guess?” Sometimes, we’ll get an estimate that is less than the true value of the population parameter, while at other times we’ll get an estimate that is greater. This is due to sampling variation. However, despite this sampling variation, our estimates will “on average” be correct and thus will be centered at the true value. This is because our sampling was done at random and thus in an unbiased fashion.

In our sampling activities, sometimes our sample proportion $\widehat{p}$ was less than the true population proportion $p$, while at other times it was greater. This was due to the sampling variability. However, despite this sampling variation, our sample proportions $\widehat{p}$ were “on average” correct and thus were centered at the true value of the population proportion $p$. This is because we mixed our bowl before taking samples and thus the sampling was done at random and thus in an unbiased fashion. This is also known as having an accurate estimate.

What was the value of the population proportion $p$ of the $N$ = 2400 balls in the actual bowl that were red? There were 900 red balls, for a proportion red of 900/2400 = 0.375 = 37.5%! How do we know this? Did the authors do an exhaustive count of all the balls? No! They were listed in the contents of the box that the bowl came in! Hence we were able to make the contents of the virtual bowl match the tactile bowl:

bowl %>% 
  summarize(sum_red = sum(color == "red"), 
            sum_not_red = sum(color != "red"))

# A tibble: 1 x 2
  sum_red sum_not_red
    <int>       <int>
1     900        1500

Let’s re-display our sampling distributions from Figures 8.12 and 8.14, but now with a vertical red line marking the true population proportion $p$ of balls that are red = 37.5% in Figure 8.15. We see that while there is a certain amount of error in the sample proportions $\widehat{p}$ for all three sampling distributions, on average the $\widehat{p}$ are centered at the true population proportion red $p$.

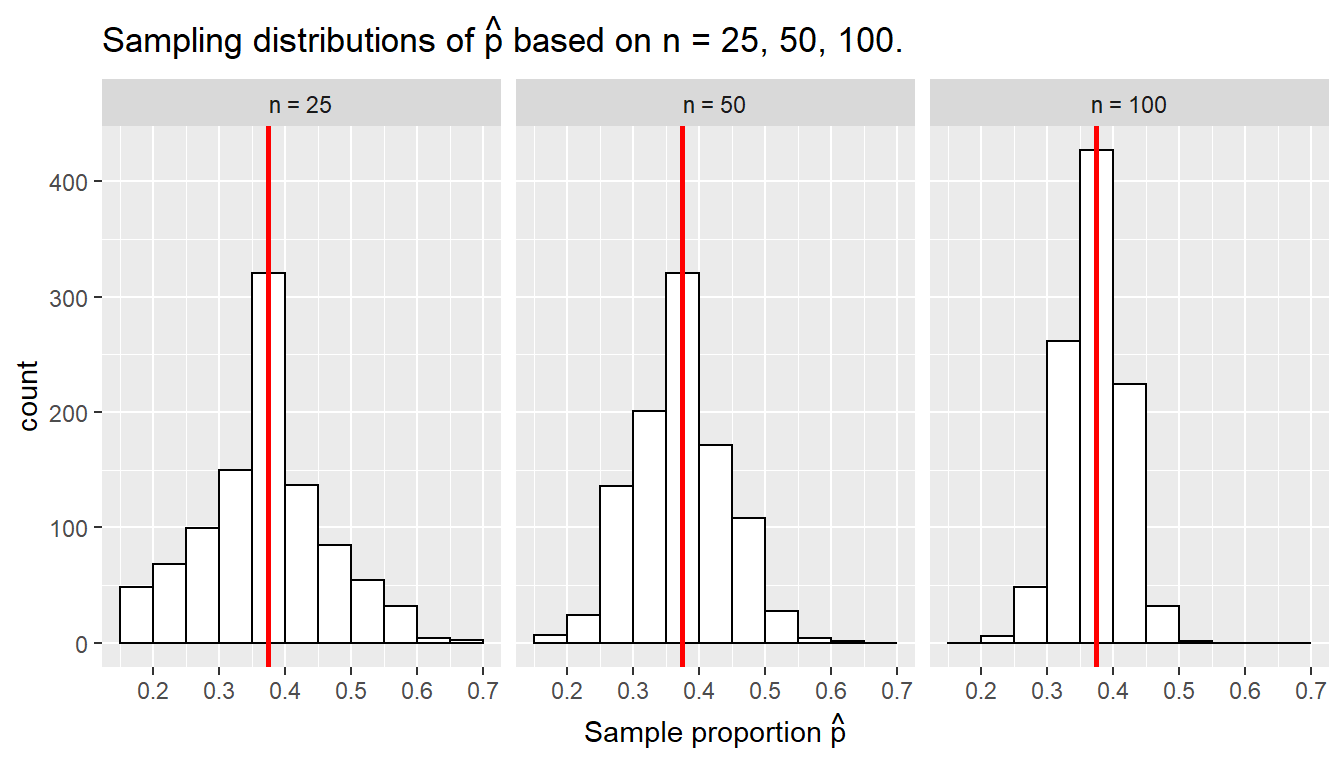
FIGURE 8.15: Three sampling distributions with population proportion $p$ marked by vertical line.

We also saw in this section that as your sample size $n$ increases, your point estimates will vary less and less and be more and more concentrated around the true population parameter. This variation is quantified by the decreasing standard error. In other words, the typical error of your point estimates will decrease. In our sampling exercise, as the sample size increased, the variation of our sample proportions $\widehat{p}$ decreased. You can observe this behavior in Figure 8.15. This is also known as having a precise estimate.

So random sampling ensures our point estimates are accurate, while on the other hand having a large sample size ensures our point estimates are precise. While the terms “accuracy” and “precision” may sound like they mean the same thing, there is a subtle difference. Accuracy describes how “on target” our estimates are, whereas precision describes how “consistent” our estimates are. Figure 8.16 illustrates the difference.

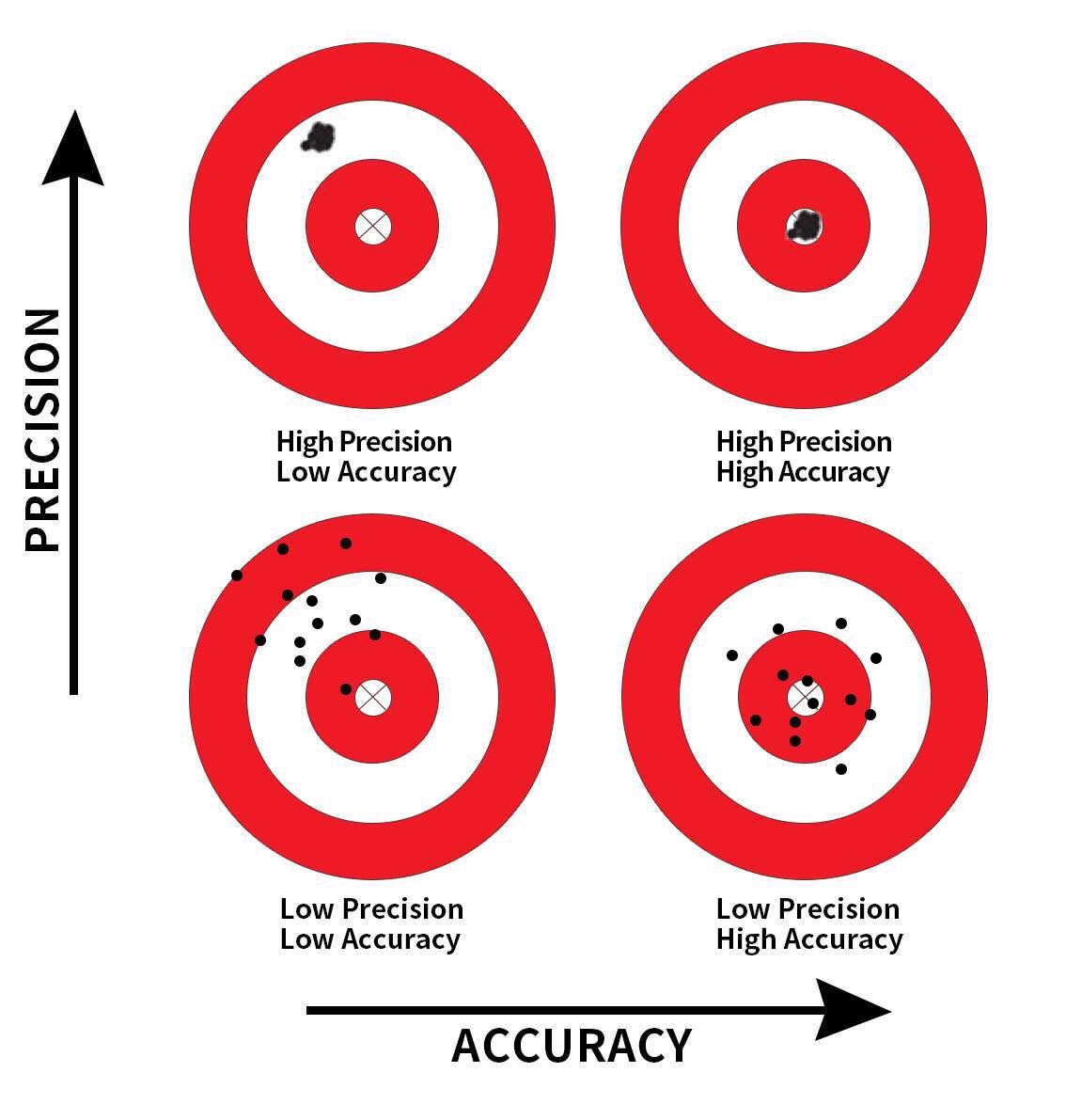
FIGURE 8.16: Comparing accuracy and precision.

At this point, you might be asking yourself: “If we already knew the true proportion of the bowl’s balls that are red was 37.5%, then why did we do any sampling?” You might also be asking: “Why did we take 1000 repeated samples of size n = 25, 50, and 100? Shouldn’t we be taking only one sample that’s as large as possible?” If you did ask yourself these questions, your suspicion is merited!

The sampling activity involving the bowl is merely an idealized version of how sampling is done in real life. We performed this exercise only to study and understand:

The effect of sampling variation.
The effect of sample size on sampling variation.

This is not how sampling is done in real life. In a real-life scenario, we won’t know what the true value of the population parameter is. Furthermore, we wouldn’t take 1000 repeated/replicated samples, but rather a single sample that’s as large as we can afford. In the next section, let’s now study a real-life example of sampling: polls.

Learning check

(LC7.16) The table that follows is a version of Table 8.3 matching sample sizes $n$ to different standard errors of the sample proportion $\widehat{p}$, but with the rows randomly re-ordered and the sample sizes removed. Fill in the table by matching the correct sample sizes to the correct standard errors.

TABLE 8.4: Standard errors of $\widehat{p}$ based on n = 25, 50, 100
Sample size	Standard error of $\widehat{p}$
n =	0.094
n =	0.045
n =	0.069

For the following four Learning checks, let the estimate be the sample proportion $\widehat{p}$: the proportion of a shovel’s balls that were red. It estimates the population proportion $p$: the proportion of the bowl’s balls that were red.

(LC7.17) What is the difference between an accurate and a precise estimate?

(LC7.18) How do we ensure that an estimate is accurate? How do we ensure that an estimate is precise?

(LC7.19) In a real-life situation, we would not take 1000 different samples to infer about a population, but rather only one. Then, what was the purpose of our exercises where we took 1000 different samples?

(LC7.20) Figure 8.16 with the targets shows four combinations of “accurate versus precise” estimates. Draw four corresponding sampling distributions of the sample proportion $\widehat{p}$, like the one in the leftmost plot in Figure 8.15.

8.4 Case study: Polls

Let’s now switch gears to a more realistic sampling scenario than our bowl activity: a poll. In practice, pollsters do not take 1000 repeated samples as we did in our previous sampling activities, but rather take only a single sample that’s as large as possible.

On December 4, 2013, National Public Radio in the US reported on a poll of President Obama’s approval rating among young Americans aged 18-29 in an article, “Poll: Support For Obama Among Young Americans Eroding.” The poll was conducted by the Kennedy School’s Institute of Politics at Harvard University. A quote from the article:

After voting for him in large numbers in 2008 and 2012, young Americans are souring on President Obama.

According to a new Harvard University Institute of Politics poll, just 41 percent of millennials — adults ages 18-29 — approve of Obama’s job performance, his lowest-ever standing among the group and an 11-point drop from April.

Let’s tie elements of the real-life poll in this news article with our “tactile” and “virtual” bowl activity from Sections 8.1 and 8.2 using the terminology, notations, and definitions we learned in Section 8.3. You’ll see that our sampling activity with the bowl is an idealized version of what pollsters are trying to do in real life.

First, who is the (Study) Population of $N$ individuals or observations of interest?

Bowl: $N$ = 2400 identically sized red and white balls
Obama poll: $N$ = ? young Americans aged 18-29

Second, what is the population parameter?

Bowl: The population proportion $p$ of all the balls in the bowl that are red.
Obama poll: The population proportion $p$ of all young Americans who approve of Obama’s job performance.

Third, what would a census look like?

Bowl: Manually going over all $N$ = 2400 balls and exactly computing the population proportion $p$ of the balls that are red.
Obama poll: Locating all $N$ young Americans and asking them all if they approve of Obama’s job performance. In this case, we don’t even know what the population size $N$ is!

Fourth, how do you perform sampling to obtain a sample of size $n$?

Bowl: Using a shovel with $n$ slots.
Obama poll: One method is to get a list of phone numbers of all young Americans and pick out $n$ phone numbers. In this poll’s case, the sample size of this poll was $n = 2089$ young Americans.

Fifth, what is your point estimate (AKA sample statistic) of the unknown population parameter?

Bowl: The sample proportion $\widehat{p}$ of the balls in the shovel that were red.
Obama poll: The sample proportion $\widehat{p}$ of young Americans in the sample that approve of Obama’s job performance. In this poll’s case, $\widehat{p} = 0.41 = 41\%$, the quoted percentage in the second paragraph of the article.

Sixth, is the sampling procedure representative?

Bowl: Are the contents of the shovel representative of the contents of the bowl? Because we mixed the bowl before sampling, we can feel confident that they are.
Obama poll: Is the sample of $n = 2089$ young Americans representative of all young Americans aged 18-29? This depends on whether the sampling was random.

Seventh, are the samples generalizable to the greater population?

Bowl: Is the sample proportion $\widehat{p}$ of the shovel’s balls that are red a “good guess” of the population proportion $p$ of the bowl’s balls that are red? Given that the sample was representative, the answer is yes.
Obama poll: Is the sample proportion $\widehat{p} = 0.41$ of the sample of young Americans who supported Obama a “good guess” of the population proportion $p$ of all young Americans who supported Obama at this time in 2013? In other words, can we confidently say that roughly 41% of all young Americans approved of Obama at the time of the poll? Again, this depends on whether the sampling was random.

Eighth, is the sampling procedure unbiased? In other words, do all observations have an equal chance of being included in the sample?

Bowl: Since each ball was equally sized and we mixed the bowl before using the shovel, each ball had an equal chance of being included in a sample and hence the sampling was unbiased.
Obama poll: Did all young Americans have an equal chance at being represented in this poll? Again, this depends on whether the sampling was random.

Ninth and lastly, was the sampling done at random?

Bowl: As long as you mixed the bowl sufficiently before sampling, your samples would be random.
Obama poll: Was the sample conducted at random? We can’t answer this question without knowing about the sampling methodology used by Kennedy School’s Institute of Politics at Harvard University. We’ll discuss this more at the end of this section.

In other words, the poll by Kennedy School’s Institute of Politics at Harvard University can be thought of as an instance of using the shovel to sample balls from the bowl. Furthermore, if another polling company conducted a similar poll of young Americans at roughly the same time, they would likely get a different estimate than 41%. This is due to sampling variation.

Let’s now revisit the sampling paradigm from Subsection 8.3.1:

In general:

If the sampling of a sample of size $n$ is done at random, then
the sample is unbiased and representative of the population of size $N$, thus
any result based on the sample can generalize to the population, thus
the point estimate is a “good guess” of the unknown population parameter, thus
instead of performing a census, we can infer about the population using sampling.

Specific to the bowl:

If we extract a sample of $n = 50$ balls at random, in other words, we mix all of the equally sized balls before using the shovel, then
the contents of the shovel are an unbiased representation of the contents of the bowl’s 2400 balls, thus
any result based on the shovel’s balls can generalize to the bowl, thus
the sample proportion $\widehat{p}$ of the $n = 50$ balls in the shovel that are red is a “good guess” of the population proportion $p$ of the $N = 2400$ balls that are red, thus
instead of manually going over all 2400 balls in the bowl, we can infer about the bowl using the shovel.

Specific to the Obama poll:

If we had a way of contacting a randomly chosen sample of 2089 young Americans and polling their approval of President Obama in 2013, then
these 2089 young Americans would be an unbiased and representative sample of all young Americans in 2013, thus
any results based on this sample of 2089 young Americans can generalize to the entire population of all young Americans in 2013, thus
the reported sample approval rating of 41% of these 2089 young Americans is a good guess of the true approval rating among all young Americans in 2013, thus
instead of performing an expensive census of all young Americans in 2013, we can infer about all young Americans in 2013 using polling.

So as you can see, it was critical for the sample obtained by Kennedy School’s Institute of Politics at Harvard University to be truly random in order to infer about all young Americans’ opinions about Obama. Was their sample truly random? It’s hard to answer such questions without knowing about the sampling methodology they used. For example, if this poll was conducted using only mobile phone numbers, people without mobile phones would be left out and therefore not represented in the sample. What about if Kennedy School’s Institute of Politics at Harvard University conducted this poll on an internet news site? Then people who don’t read this particular internet news site would be left out. Ensuring that our samples were random was easy to do in our sampling bowl exercises; however, in a real-life situation like the Obama poll, this is much harder to do.

Learning check

Comment on the representativeness of the following sampling methodologies:

(LC7.21) The Royal Air Force wants to study how resistant all their airplanes are to bullets. They study the bullet holes on all the airplanes on the tarmac after an air battle against the Luftwaffe (German Air Force).

(LC7.22) Imagine it is 1993, a time when almost all households had landlines. You want to know the average number of people in each household in your city. You randomly pick out 500 phone numbers from the phone book and conduct a phone survey.

(LC7.23) You want to know the prevalence of illegal downloading of TV shows among students at a local college. You get the emails of 100 randomly chosen students and ask them, “How many times did you download a pirated TV show last week?”

(LC7.24) A local college administrator wants to know the average income of all graduates in the last 10 years. So they get the records of five randomly chosen graduates, contact them, and obtain their answers.

8.5 Conclusion

8.5.1 Sampling scenarios

In this chapter, we performed both tactile and virtual sampling exercises to infer about an unknown proportion. We also presented a case study of sampling in real life with polls. In each case, we used the sample proportion $\widehat{p}$ to estimate the population proportion $p$. However, we are not just limited to scenarios related to proportions. In other words, we can use sampling to estimate other population parameters using other point estimates as well. We present four more such scenarios in Table 8.5.

TABLE 8.5: Scenarios of sampling for inference
Scenario	Population parameter	Notation	Point estimate	Symbol(s)
1	Population proportion	$p$	Sample proportion	$\widehat{p}$
2	Population mean	$\mu$	Sample mean	$\overline{x}$ or $\widehat{\mu}$
3	Difference in population proportions	$p_1 - p_2$	Difference in sample proportions	$\widehat{p}_1 - \widehat{p}_2$
4	Difference in population means	$\mu_1 - \mu_2$	Difference in sample means	$\overline{x}_1 - \overline{x}_2$
5	Population regression slope	$\beta_1$	Fitted regression slope	$b_1$ or $\widehat{\beta}_1$

In the rest of this book, we’ll cover all the remaining scenarios as follows:

In Chapter 9, we’ll cover examples of statistical inference for
- Scenario 2: The mean age $\mu$ of all pennies in circulation in the US.
- Scenario 3: The difference $p_1 - p_2$ in the proportion of people who yawn when seeing someone else yawn first minus the proportion of people who yawn without seeing someone else yawn first. This is an example of two-sample inference.
In Chapter 10, we’ll cover an example of statistical inference for
- Scenario 4: The difference $\mu_1 - \mu_2$ in mean IMDb ratings for action and romance movies. This is another example of two-sample inference.
In Chapter 11, we’ll cover an example of statistical inference for regression by revisiting the regression models for teaching score as a function of various instructor demographic variables you saw in Chapters 6 and 7.
- Scenario 5: The slope $\beta_1$ of the population regression line.

8.5.2 Central Limit Theorem

What you visualized in Figures 8.12 and 8.14 and summarized in Tables 8.1 and 8.3 was a demonstration of a famous theorem, or mathematically proven truth, called the Central Limit Theorem. It loosely states that when sample means are based on larger and larger sample sizes, the sampling distribution of these sample means becomes both more and more normally shaped and more and more narrow.

In other words, their sampling distribution increasingly follows a normal distribution and the variation of these sampling distributions gets smaller, as quantified by their standard errors.

Shuyi Chiou, Casey Dunn, and Pathikrit Bhattacharyya created a 3-minute and 38-second video at https://youtu.be/jvoxEYmQHNM explaining this crucial statistical theorem using the average weight of wild bunny rabbits and the average wingspan of dragons as examples. Figure 8.17 shows a preview of this video.

FIGURE 8.17: Preview of Central Limit Theorem video.

8.5.3 Additional resources

An R script file of all R code used in this chapter is available here.

8.5.4 What’s to come?

Recall in our Obama poll case study in Section 8.4 that based on this particular sample, the best guess by Kennedy School’s Institute of Politics at Harvard University of the U.S. President Obama’s approval rating among all young Americans was 41%. However, this isn’t the end of the story. If you read the article further, it states:

The online survey of 2,089 adults was conducted from Oct. 30 to Nov. 11, just weeks after the federal government shutdown ended and the problems surrounding the implementation of the Affordable Care Act began to take center stage. The poll’s margin of error was plus or minus 2.1 percentage points.

Note the term margin of error, which here is “plus or minus 2.1 percentage points.” Most polls won’t produce an estimate that’s perfectly right; there will always be a certain amount of error caused by sampling variation. The margin of error of plus or minus 2.1 percentage points is saying that a typical range of errors for polls of this type is about $\pm$ 2.1%, in words from about 2.1% too small to about 2.1% too big. We can restate this as the interval of $[41\% - 2.1\%, 41\% + 2.1\%] = [37.9\%, 43.1\%]$ (this notation indicates the interval contains all values between 37.9% and 43.1%, including the end points of 37.9% and 43.1%). We’ll see in the next chapter that such intervals are known as confidence intervals.

Scenario	Population parameter	Notation	Point estimate	Symbol(s)
1	Population proportion	\(p\)	Sample proportion	\(\widehat{p}\)
2	Population mean	\(\mu\)	Sample mean	\(\overline{x}\) or \(\widehat{\mu}\)
3	Difference in population proportions	\(p_1 - p_2\)	Difference in sample proportions	\(\widehat{p}_1 - \widehat{p}_2\)
4	Difference in population means	\(\mu_1 - \mu_2\)	Difference in sample means	\(\overline{x}_1 - \overline{x}_2\)
5	Population regression slope	\(\beta_1\)	Fitted regression slope	\(b_1\) or \(\widehat{\beta}_1\)